where A, B and C are constants, find the value of A and B and show that C = 0.
(ii) Differentiate ln(x2 + 4) with respect to x.
(iii) Using the results from parts (i) and (ii), find(i) Since
Equating coefficients of x2, we have
A + 2B = 3 --- (1)
Equating coefficients of x, we get
B + 2C = 4 --- (2)
Equating constants, we have
4A + C = -20 ----(3)
From (1), A = 3 – 2B --- (4)
Sub (4) into (3), we get 4(3 – 2B) + C = - 20
12 – 8B + C = -20
-8B + C = -32 ---(5)
B + 2C = 4 --- (2)
(5) x 2 -16B + 2C = -64 --- (6)
(2) – (6) 17B = 68
B = 4
Sub B = 4 into (2), we get C = 0 (shown)
From (3) 4A = -20
A = -5
Hence, A = -5, B = 4 and C = 0




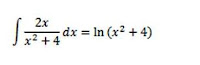
No comments:
Post a Comment